完全负相关(r
AB=-1)时,两种证券组合的标准差=|W
Aσ
A-W
Bσ
B|,此时风险分散效应最强,存在使“组合风险=0”的组合,机会集如图所示:
)j���U)_To 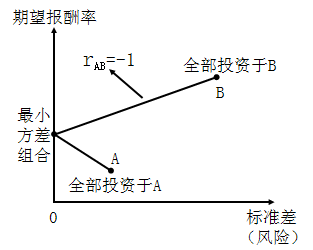 52Sa�KA[��
52Sa�KA[�� 显然,在两种证券完全负相关时,机会集是一条向左弯曲(向A点左侧凸出)的曲线,并与纵轴有唯一的交点,其含义如下:
o�}$XH,-9& 1)两种证券完全负相关时,存在唯一能使组合标准差=0的组合(满足W
A/W
B =σ
B/σ
A)——最小方差组合,即图中机会集曲线与纵轴的交点。
qS403+Su1= ①最小方差组合:机会集中风险最低的组合,是机会集中最左端的点,该组合所带来的预期收益率,是投资者投资于A、B两种证券组合所能接受的最低收益率(必要收益率);
�W0y� '5�` ②由于组合的预期收益是组合内各证券预期收益的加权平均值,因此,图中A点(全部资金投资于低风险、低收益的A证券)是机会集中预期收益最小的组合,是机会集中最下端的点,任何同时投资于A、B两种证券的组合,其预期收益率都将高于A点,因此,最小方差组合位于A点的左上方。
�#Vl 0�.l3 2)风险分散化效应
w Qgo�N%�� A点~最小方差组合之间的曲线向左上方弯曲,表明拿出一部分资金投资于高风险、高收益的B证券,所形成的组合比全部资金都投资于风险较低的A证券(A点)具有更低的风险(一部分特殊风险被分散掉)和更高的收益,也说明存在比低风险的证券A的风险还要低的投资组合。
)`�SE�S�." 3)有效集与无效集
��i�W�e�i� ①无效集:最小方差组合以下的组合,图中A点~最小方差组合之间的曲线;
?{�\nf7�Y 预期收益率<必要收益率(最小方差组合的预期收益率)
m`IC�6���* 与最小方差组合相比,风险大、收益低
�{G|,�\�O1 ②有效集:最小方差组合以上的组合,从最小方差组合(风险最低)到最高预期收益组合(收益最高)的一段曲线,图中最小方差组合~B点之间的曲线。